CHARLES-ANGE LAISANT

Basse-Indre 1841 – Asnières-sur-Seine 1920

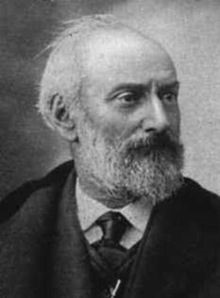
• Brief professional biography
• Involvement in French politics
• Commitment to education
• Bibliography
• Books on the teaching of mathematics

Brief professional biography

Charles-Ange Laisant is remembered for his deep commitment to the advancement of mathematics teaching, for his role in the creation of important mathematical journals, and for his contributions to the development of a truly international mathematical community.
Laisant was born on 1 November, 1841, in the small village of Basse-Indre, some 10 Km West of Nantes, the site of a foundry founded in the 1820s. He studied at the école Polytechnique, Paris, and later at the école d’Application, Metz. In 1871 he received the Croix de la Legion d’honneur for his role in the defense of the fortress of Issy, at the time of the siege of Paris in the final stages of the Franco-Prussian war. At the end of that war Laisant, and a group of his immediate friends, were left with a sense that an effort should be made to restore their country to the position it occupied in the intellectual life of the nations of Europe in the early years of the century, and to break with what they perceived as its cultural isolation. They shared the belief that some basic changes were necessary in the structure of French society; they did not exclude the French scientific community from being also in need of renovation. They believed that the structure of the latter was antiquated and lacked in communication facilities; that there was a weak integration between science and society, and also between the capital and the departments. In their perception, the situation was different in Germany; some even cited those facts as being among the main causes of the Prussian victory. These understandings had a substantial impact on the personal and scientific life of Laisant and of some of his friends, who later made considerable efforts to renovate the scientific community of their country and to set it on a more internationalist path. If they played a role in the 1870 war, on occasions of significance as it was the case of Laisant, their actions after that war had a far more permanent impact on the life of their country. It is not then surprising that the period immediately after the Franco-Prussian war was one of substantial institutional development. In it a serious effort was made to bring about an avancement of science through a more organized and planned development, in an almost industrial scale. In rapid succession, which contrasts with earlier periods, new societies for the promotion of science either in general or in specific branches were created. These new institutions nurtured either closer scientific relations between Paris and the rest of the country, as was the case of the Assoçiation Francaise pour l'Avancement des Sciences; attempted to contribute to the development of specific branches of science at research level, as was the case of Société de Physique and the Société Mathématique de France; or promoted the teaching of science and mathematics in a more modern style than ever before. In all cases, these organizations quickly opened contacts with their sisters abroad. The circle of scientists to which Laisant belonged also promoted a wider exchange of ideas and a better understanding between science and its social and political context. In a second stage, towards the end of the century, they embarked on new projects to promote wider channels of international scientific contact and communication and to improve mathematics education. Laisant’s life, as a mathematician, as a promoter of the development of the mathematical community and of modern mathematics education, and as a politician, is paradigmatic of this important period in France’s intellectual history. Laisant had a genuine interest in mathematical research and contributed to a number of contemporaneous mathematics periodicals on topics of analysis, mechanics and geometry, the latter was his main and lasting interest. He was not, however, a leading member of the French mathematics research elite of his time. On a personal level, his contemporaries describe him as a warm, generous and independent man; many pages of his work and of his actions in life suggest this description may have been accurate. He was also a truly European character and a committed pacifist, who championed for closer international contacts, particularly between France and Germany. Laisant died in Paris in 1920 after seeing the horror of the First World and the division it created in an international mathematical community he had contributed to create and that he fostered over the years; however, even after renewed catastrophes, many of his ideas have lived on.
In addition, through the last third of the nineteenth century, Laisant and his friends, particularly émile Lemoine (1840-1912), contributed significantly to the development of a branch of classical geometry concerned with the detailed study of the ‘special points’ of the triangle, the so-called Geometry of the Triangle. The development of this chapter of geometry is directly related to new ideas in the field of mathematics education that advocated the eradication of a memoirist teaching of Euclidean geometry which, they rightly claimed, did not foster creativity in the minds of students. The recitation of Euclid texts almost by heart was grounded on the belief that nothing could be altered in its already perfect formulation. By contrast, the profusion of geometrical properties brought about by the geometry of the triangle allowed teachers to propose to their students problems leading to the discovery of new- even if often not necessarily deep- geometrical results. This, they believed, would take out of the student’s mind the idea that geometry, and more generally mathematics, is a dead science in which advance is not anymore possible. In the early 1870s, Capitaine de Génie Laisant’s main research interest was the theory of curves and surfaces, where the possibility of using the methodology of vector calculus to simplify proofs was beginning to be considered. Most of his mathematical work was done while he was Examinateur d’admission or Repétiteur at the école Polytechnique, Paris. Through the work of Guillaume-Jules Hoüel (1823-1886), Laisant was initially attracted to the new ideas on equipollences, a concept developed in Italy from the 1850 by Giusto Bellavitis (1803-1880). He perceived the power of that new tool, capable of giving plane geometry a ‘calculus’ with operational rules related to those of ordinary algebra. In the early 1870s he entered into correspondence with Bellavitis and translated into French, adding extensive historical and technical notes, Bellavitis’ Exposition de la méthode des équipollences; the book, published by the new firm of Gauthier-Villars in 1874, had a considerable impact in France. However, essential difficulties were soon encountered when trying to extend equipollences to three-dimensional space. These complications made Laisant, as well as Hoüel and Bellavitis himself, turn their attention to William Hamilton’s (1805-1865) new work on quaternions. Hoüel devoted the fourth volume of his treatise on complex quantities, published in 1874, to a discussion on these new mathematical objects. Three years later, when Laisant submitted a thesis to the Faculté des Sciences, Paris, for a doctorat des sciences, he discussed quaternions and their applications to mechanics. Laisant stated in his work that Hoüel had been his main advisor and relied on Hoüel’s treatise as a background for his own work. However, at the time Laisant still regarded the theory of quaternions as a spatial extension of a Bellavitis’s calculus, which required the introduction of special algebraic rules.
Although Laisant was clearly not the first to consider quaternions in France, he was a pioneer in the process of its transmission to his country. In 1881 he published an elementary treatise on Hamilton’s quaternions, far more readable than Hoüel’s introduction of 1874. In this work he followed the textbook of Philip Kelland (1808-1879) and Peter Guthrie Tait (1831-1901), Introduction to quaternions, published in 1880 in London. However, Laisant's book is more that a free translation of that book, his treatment some topics has more depth and elegance. There was however a serious problem with quaternions: they allow for a three dimensional extension retaining the ordinary operations of addition and subtraction, but it was soon found out that there was some freedom in the definition of multiplication: If a division algebra was to be retained, it was necessary to define for the basic units i, j, k, a multiplication table such that i2 = j2 = k2 = -1, ij = k, while ji = -k, and so by cyclic permutation. If the more symmetric law ij = ji was adopted, it was easy to find non-zero quaternions, whose product was equal to zero. This forced the choice a multiplication table that breaks the analogy with ordinary algebra. Laisant remarked that the loss of commutativity created ‘difficultés spéciales’ (p. ix), as it made the concept quaternions far more difficult to grasp, but he believed that this was a consequence of the intrinsic geometrical characteristics of three-dimensional space: ‘Mais cet inconvénient résulte de la nature même des choses. Il représente la traduction exacte, formelle, d'un fait précis.’ (p. ix).
Returning to the question of scientific isolation, in his doctoral dissertation, as well as in other work, Laisant attempted to discuss the reasons for what he regarded as a long delay in the transmission of the theory of quaternions to France. He believed the exclusively analytical way in which they had been presented to French readers was a main factor; because of this perception in his work he emphasized the geometric side of quaternions. This emphasis is visible in his definition of quaternions in terms of the biradiale, that is, introducing the quaternions as a quotient of vectors which, sadly, may not have been the best approach. Laisant also remarked on the different status geometry and analysis had in France in the years immediately after the Franco-Prussian war. In correspondence to other French mathematicians he indicated that opposition to vectors had been strong in the upper echelons of French mathematics in the 1880s, and that through the 1890s research topics on analysis were far more highly regarded than those related to geometry. The books of Hoüel and Laisant, and Gustave Plarr's direct translation of Kelland and Tait’s treatise into French facilitated the reception of the theory quaternions in France through the 1870s and 1880s.
In the preface to his textbook on quaternions, Laisant indicated that it was written as the result of the insistence of some of his friends, who believed the quaternions cause might benefit from the availability of an easily accessible and concise introductory textbook. Laisant also claimed that he had written this book in the three years following the presentation of his doctoral dissertation, and that it was written in the few moments left to him by his present duties. In it he described them as ‘multiples et fort étrangères aux Mathématiques.’ (p. v). Indeed they were.

Involvement in French politics

In the same years Laisant battled for the reception of equipollences and quaternions in France, he was fully committed to national politics. His political career started at a local level in Nantes in 1871; three years later he was reelected as a candidate of a left-republican party (Union Républicaine) founded by Léon-Michel Gambetta (1838-1882), later Premier of France. This is precisely the period when Laisant translated Bellavitis. Two years later he broke with his party beating the official candidate in the national February-March 1876 elections as a representative of the extreme left; on that year he resigned his commission in the army and in 1877 joined the national Chamber as a Député. This was also the year Laisant submitted his doctoral dissertation to the Faculté des Sciences, Paris.
In 1879 Laisant became the director of the political journal Le Petit Parisien and in the following year he was sentenced for publishing articles attacking a leading official figure in the French army. In December 1880 Laisant finished writing his textbook on quaternions, which was published in 1881; it was in this book that he made the remark on his non-mathematical activities. In 1882 he became a Député for the Département de Loire-Inférieure and from then on his political career continued with a rapid progression, but not without conflict either. In 1883 an article of his, published in another fringe political journal, La République Radical, caused new serious conflicts. In 1885 Laisant was re-elected as a member of Parliament, but now for the Seine constituency of Paris. In the meantime a new political figure, War Minister General Georges Boulanger (1837-1891), appeared in the French political scene at a time the Premier was the polytechnicien and mathematician Charles de Freycinet (1828-1923). Laisant's relations with Boulanger began before 1887, when he was active in parliamentary commissions working on a project on conscription and the reorganization of the army, an area in which he had considerable professional experience. Minister Boulanger proposed several reforms, some controversial, such as transforming the école Polytecnique into a national engineering school, away from army control. He was soon forced to resign, but began to be considered as a possible national political figure capable of effecting change. A political alliance of groups holding very different views and objectives was formed around him; Laisant supported it. The contradictions inherent to such complex alliance would soon become visible and ended in electoral disaster in 1889; deeply discredited and troubled by personal problems, Boulanger took his own life. Although affected in his political credibility by this disaster, Laisant still won a parliamentary seat for the Paris XVIII-ème arrondissement against the official socialist candidate in 1889. However, in 1893, after twenty years, he decided to quit French national politics. His resignation from politics, where he had acquired valuable organization skills and multiple personal contacts, would have some deep consequences for the development of an international mathematical community.
Laisant was also involved in an effort to give the international mathematical community a more structured organization and promote personal contacts through regular international meetings of mathematicians. This initiative led to the regular meetings which today are sponsored by the International Mathematical Union. After its first official Congress in Paris in 1900, and following a suggestion made by Ferdinand Rudio (1856-1929) at the Zürich meeting of 1897 Laisant, with the assistance of the Geneva mathematician Adolphe Buhl (1878-1949), compiled a world list of individuals interested in mathematics: the Annuaire des Mathématiciens, 1901-1902. The list was supposed to be reviewed annually but sadly this did not happen.

Commitment to education

At a meeting of the Association Française pour l’Avancement des Sciences in August 1894, at Caen, Laisant announced the foundation of a journal open to the international community and designed to share information between readers. Any subscriber with a definite mathematics question could submit it to the journal in the hope that some other reader knowing the answer would print it. The name of this journal was L’Intermédiaire des Mathématiciens. It was modeled on a successful British journal for the generally educated public founded in the 1840, which had inspired similar journals in different countries of Europe and America. Five years later, in 1899 Laisant founded yet another mathematical journal, L'Enseignement Mathématique, designed to promote closer contacts between those engaged in mathematics teaching, and to serve as a forum for the discussion of new pedagogical ideas; Henri Fehr (1870-1954), from Geneva, was his co-editor. When the Commission Internationale de l'Enseignement Mathématique was founded in 1908, L’Enseignement Mathématique became its official journal. In those years he was one of the editors of the journal Nouvelles Annales de Mathématiques.
In November 1888 the French government created an official committee for the organization of an international congress on mathematical bibliography; the congress met in Paris one year later. Following this initiative, an international permanent committee was later created and Henri Poincaré (1854-1912) was designated its president, with Laisant as secretary. The commission published an index of the Répertoire Bibliographique des Sciences Mathématiques, and established a national committee with representatives from Europe and the United States. For this commission Laisant introduced a new classification methodology in which he made use of the idea of re-directing searches (système de renvois).
Laisant was also the author of several general books on mathematics and mathematics education, among them: La Mathématique, Philosophie, Enseignement, Paris, 1898 and L’Initiation Mathématique, Paris, 1910, which were reprinted many times and had some influence on mathematics education though the world. In them he attempted to bring the ideas of philosopher Auguste Comte into a mathematical context. However, his approach was not uncritical; Laisant remarked that the definition of mathematics as the science dealing with the indirect measurement of magnitudes, given by the master in his works, was insufficient: Laisant stressed that mathematics deals also with the important notion of order, which he saw as inherent to mathematics as that of measurement. In 1903-1904 Laisant was elected president of the Assoçiation Francaise pour l'Avancement des Sciences, he was also elected vice-president of the Société Astronomique de France and was also honored by leading societies and academies. In 1904, in the Bulletin of the Société Astronomique, Laisant wrote an interesting piece on the social role of science, in which he anticipated some arguments considered in the 1930s controversy on science and society.
Laisant, as well as some of his friends, particularly Lemoine, had a serious interest in chamber music; with other polytechniciens he founded a music circle known as La Trompette, which met regularly. It included Camille Saint-Saëns (1835-1921) among its musical members and Poincaré among the mathematical ones.
On Laisant’s death, in an obituary written in 1920, his collaborator and friend Buhl referred to ‘l’esprit logique, idéaliste et révolutionnaire de Laisant’. In his time, contrary to a ‘Darwinian’ world-view based on fierce competition, Laisant and his friends attempted to construct a community in which cooperation and association was the rule.

Bibliography

S. ALTMANN, E. L. ORTIZ (editors) 2005, Mathematics and social utopias in France: Olinde Rodrigues, Providence, American Mathematical Society/ London Mathematical Society.
J. AUVINET 2013, Charles-Ange Laisant. Itinéraires et engagements d’un mathématicien de la Troisième République, Paris, Hermann.
G. BELLAVITIS 1874, Exposition de la méthode des équipollences, traduit de l'Italien par M. Laisant, Gauthier-Villars, Paris. (This work was first serialized in Nouvelles Annales de Mathématiques).
A. BUHL 1920, Charles-Ange Laisant, L’Enseignement Mathématique, 21, 73-80.
P. FREGUGLIA 1991, I fondamenti dell’algebra degli immaginari secondo Giusto Bellavitis, M. GALUZZI (editor), Giornate di storia della matematica, Rende, Editel, 143-168.
F. FURINGHETTI 2003, Mathematical instruction in an international perspective: the contribution of the journal L’Enseignement mathématique, in D. CORAY, F. FURINGHETTI, H. GISPERT, B. R. HODGSON, G. SCHUBRING (editors), One hundred years of L’Enseignement Mathématique, Monographie n. 39, L’Enseignement Mathématique, 19-46.
H. GISPERT 1991, La France Mathématique de France (1872–1914) , Cahiers d’Histoire et de Philosophie des Sciences, Nouvelle Série, 34(1), 297–322.
H. GISPERT 2002. Par la science, pour la patrie: L’Association Française pour l’Avancement des Sciences, Rennes, Les Presses Universitaires de Rennes.
C.–A. LAISANT 1880, Giusto Bellavitis, Bulletin des Sciences Mathématiques, 2ème série, 4, 343-348.
C.–A. LAISANT 1881, Introduction à la méthode des quaternions, Paris, Gauthier-Villars.
C.–A. LAISANT 1887, Théorie et applications des équipollences, Paris, Gauthier-Villars.
C.–A. LAISANT 1887, Assemblé Nationale, Chambre des députés. Commission chargée d'examiner le projet de loi organique militaire, Rapport par le député M. Ch.-A. Laisant, Paris, Imprimerie de la Chambre des Députés.
E. L. ORTIZ 1996, The nineteenth-century international mathematical community and its connection with those on the Iberian periphery, in J. GRAY, C. GOLDSTEIN, J. RITTER (editors), L'Europe Mathématique, Paris, Edition de la Maison des Sciences, 321-344.
E. L. ORTIZ 1999, Quaternions abroad: some remarks on their impact in France, Acta Historiae Naturalium Necnon Technicarum, 3, 295–302.
E. L. ORTIZ 2001, Proyectos de cambio científico y proyectos de cambio político en la tercera República: el caso de la teoría de los cuaterniones, Revista Brasileira de História da Matemática, 1, 66–85. Also in: El valor de las matemáticas, In A. DURAN, J. FERREIROS (editors), Sevilla, 141–164.
E. L. ORTIZ 2007, Babbage and French idéologie: functional equations, language and the analytical method, Chapter 2, in J. GRAY, K. PARSHALL (editors), Episodes in the History of Modern Algebra (1800-1950), Providence and London, American Mathematical Society/ London Mathematical Society.
M. ZERNER 1991, Le règne de Joseph Bertrand (1874–1900), Cahiers d’Histoire et de Philosophie des Sciences, Nouvelle Série, 34, 298–322.

Books on the teaching of mathematics

C.-A. LAISANT 1898, La mathématique: philosophie-enseignement, Paris, G. Carré et C. Naud.
C.–A. LAISANT 1906, L'éducation de demain, Philosophie libertaire. Second edition in 1913, Paris, Les temps nouveaux
C.–A. LAISANT 1910, L’Initiation mathématique, Paris, Hachette.
With H. Delannoy and é. Lemoine, Laisant edited:
E. LUCAS 1895, L'arithmétique amusante, Paris, Gauthier-Villars et fils.
E. LUCAS 1891-96, Récréations mathématiques, Paris, Gauthier-Villars.


Author
Eduardo L. Ortiz
Imperial College, London
e.ortiz@imperial.ac.uk

Editors: Fulvia Furinghetti (Università di Genova) and Livia Giacardi (Università di Torino)
Multimedia Author: Tiziana Armano (Università di Torino)
Copyright © 2008-2028 Dipartimento di Matematica - Università di Torino - Last update: 27/03/2020